Lesson 1: Preparing for Success
Opening Video
In a BYU-Idaho devotional President Russel M. Nelson shared his thoughts about the potential of BYU-Idaho students. As you watch this four minute clip, pay attention to what President Nelson says BYU-Idaho students can accomplish.
Russell M. Nelson “The Lord Uses the Unlikely to Accomplish the
Impossible”
(4:44
mins, Nelson Excerpt Transcript)
Introduction
As mentioned by President Nelson, “the Lord has more in mind for you than you have in mind for yourself.” In this course, Math 108X: Mathematical Tools for the Real World, we will learn tools that can help you be prepared to make informed decisions. As you make informed decisions you will be able to do as promised by President Nelson and “accomplish the impossible.”
Tips for Success
Read the Textbook This online textbook has been prepared as a resource to help you succeed in this class. Please take the time to carefully read the assigned reading each week.
Work through the Textbook As you read the textbook, realize that you can’t read a math textbook the same way you do a novel. As you complete the reading assignments, read with a paper and pencil and Excel nearby. As you read, take notes on important principles and concepts. When you encounter an example or interactive problem in the text, work the example out on paper and make sure you could repeat the example again on your own. When you are given instructions for how to do something in Excel, open Excel on your computer and follow along with the instructions.
How Did I Do? The homework assignments and Excel case studies include a “How Did I Do” button or tab that allows you to check your work. Use these tools appropriately. If you don’t get a problem correct the first time, take time to check your work. Go back and look at the reading material and see if there are concepts you need to review.
Work with Your Group Whether you are an online student working with a group online or a campus student working with a group in class, work together as a group. You will benefit as you serve others by taking time to explain principles you understand. And you will learn from others as they explain principles you are struggling to learn. Be an active and willing participant in group activities and assignments.
Notice Applications As you work on readings, homework, case studies, and exams always consider how you could apply the principles you are learning to your own life.
The goal of this course is to help you use mathematical and statistical tools to make informed decisions. Life is full of opportunities to make decisions that impact our lives.
President Henry B. Eyring, Second Counselor in the First Presidency, said “The Lord knows both what He will need you to do and what you will need to know. He is kind and He is all-knowing. So you can with confidence expect that He has prepared opportunities for you to learn in preparation for the service you will give. You will not recognize those opportunities perfectly….But when you put the spiritual things first in your life, you will be blessed to feel directed toward certain learning, and you will be motivated to work harder.”1
This course is an opportunity for you to learn to make informed decisions in your life so that you can be of better service to the Lord.
Algebraic Tools
Let’s review some algebraic tools and properties that will be helpful this semester. We will review manipulating fractions, the order of operations, and properties of exponents.
Manipulating Fractions
Fractions commonly occur in mathematical situations. Remember that a fraction is made up of one whole number divided by another. The number on the top of the fraction is called the numerator. The number on the bottom of the fraction is called the denominator.
We will review the rules we follow when adding, subtracting, multiplying and dividing fractions. These examples are brief and are just intended to be a quick review of principles you have learned before.
Adding Fractions
In order to add fractions, you first find a common denominator. Then you add the numerator and keep the common denominator of the fraction the same. Let’s look at an example.
Example 1
Add \(\frac{3}{4}+\frac{2}{3}\).
Solution:
First, we find a common denominator. In this case the denominators of the two fractions are 4 and 3. We need to find a denominator that is divisible by both 4 and 3. The smallest number that can be evenly divided by 4 and 3 is 12. So our common denominator is 12. We multiply both fractions by 1, written as a number divided by itself, so that we can get the common denominator of 12:
\[ \begin{aligned} \frac{3}{4}+\frac{2}{3}&=\frac{3}{4}\cdot\frac{3}{3}+\frac{2}{3}\cdot\frac{4}{4}\\ &=\frac{9}{12}+\frac{8}{12}\\ &=\frac{9+8}{12}\\ &=\frac{17}{12}\\ \end{aligned} \]
Notice that after we found a common denominator of 12, we added the numerators of the fractions, but kept the common denominator of 12 on the bottom of the fraction.
Example 2
Add \(\frac{17}{9}+\frac{8}{3}\).
Solution:
First, we find a common denominator. In this case the denominators of the two fractions are 9 and 3. We need to find a denominator that is divisible by both 9 and 3. The smallest number that can be evenly divided by 9 and 3 is 9. So our common denominator is 9. We multiply the second fractions by 1, written as a number divided by itself, so that we can get the common denominator of 9:
\[ \begin{aligned} \frac{17}{9}+\frac{8}{3}&=\frac{17}{9}+\frac{8}{3}\cdot\frac{3}{3}\\ &=\frac{17}{9}+\frac{24}{9}\\ &=\frac{17+24}{9}\\ &=\frac{41}{9}\\ \end{aligned} \]
Notice that after we found a common denominator of 9, we added the numerators of the fractions, but kept the common denominator of 9 on the bottom of the fraction.
Subtracting Fractions
Subtraction of fractions is very similar to adding fractions. We find a common denominator then subtract the numerators while keeping the denominator constant.
Example 3
Simplify: \(\frac{3}{8}-\frac{13}{12}\)
Solution:
For this problem, we notice that the smallest number that is divisible by both 8 and 12 is 24. So we use a common denominator of 24.
\[ \begin{aligned} \frac{3}{8}-\frac{13}{12}&=\frac{3}{8}\cdot\frac{3}{3}-\frac{13}{12}\cdot\frac{2}{2}\\ &=\frac{9}{24}-\frac{26}{24}\\ &=\frac{9-26}{24}\\ &=\frac{-17}{24}\\ \end{aligned} \]
Example 4
Simplify: \(\frac{5}{7}-\frac{5}{3}\)
Solution:
For this problem, we notice that the smallest number that is divisible by both 7 and 3 is 21. So we use a common denominator of 21.
\[ \begin{aligned} \frac{5}{7}-\frac{5}{3}&=\frac{5}{7}\cdot\frac{3}{3}-\frac{5}{3}\cdot\frac{7}{7}\\ &=\frac{15}{21}-\frac{35}{21}\\ &=\frac{15-35}{21}\\ &=\frac{-20}{21}\\ \end{aligned} \]
Multipling Fractions
To multiply fractions, we just multiply the numerators and multiply the denominators.
Example 5:
Multiply the fractions \(\frac{2}{5}\) and \(\frac{-4}{3}\).
Solution:
We multiply the fractions by multiplying the numerators and multiplying the denominators:
\[ \begin{aligned} \frac{2}{5}\cdot\frac{-4}{3}&=\frac{2\cdot(-4)}{5\cdot3}\\ &=\frac{-8}{15} \end{aligned} \]Dividing Fractions
To divide fractions, we invert and multiply. This means that we take the second fraction, flip it upside down, and then multiply the two resulting fractions.
Example 6:
Do the following: \(\frac{3}{4}\div\frac{6}{5}\).
Solution:
We perform the division by inverting the second fraction and then multiplying.
\[ \begin{aligned} \frac{3}{4}\div\frac{6}{5}&=\frac{3}{4}\cdot\frac{5}{6}\\ &=\frac{3\cdot5}{4\cdot6}\\ &=\frac{15}{24}\\ &=\frac{5}{8}\\ \end{aligned} \]Order of Operations
Have you ever come across a question like this on Facebook or other Social Media?
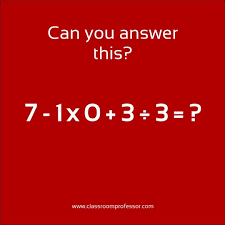
The comments on this type of social media posts typically shows great disagreement on the answer. The correct answer relies on the order of operations. The order of operations is a rule that helps us know the order in which to apply mathematical operations when simplifying an expression. The order of operations tells us to perform operations in the following order:
| Step 1: | Carry out operations enclosed in parentheses. |
| Step 2: | Carry out operations involving exponents. |
| Step 3: | Carry out any multiplication or division, in the order in which they appear from left to right. |
| Step 4: | Carry out any addition or subtraction, in the order in which they appear from left to right. |
The acronym P.E.M.D.A.S. is often used to describe the order of
operations. P.E.M.D.A.S stands for parentheses, exponents,
multiplication and division, addition and subtraction. Even though the M
appears before the D and the A appears before the S, it is essential to
remember that multiplication and division are carried out in the order
they appear from left to right. It is similarly important to carry out
addition and subtraction in the order they appear from left to right.
The acronym P.E.M.D.A.S. might be better listed as P.E.(M.D.)(A.S.) with
the parentheses reminding us that multiplication and division occur
together, as do addition and subtraction.
Examples With Integers
Example 7
Apply the order of operations to the Facebook meme posted above:
\[ 7-1\times 0 + 3\div 3 \]
Solution
Steps 1 and 2 don’t apply because there are no parentheses or exponents. So we start with Step 3 and perform all multiplication and division in the order in which they appear from left to right. Because \(1 \times 0=0\) and \(3 \div 3=1\) we can rewrite the equation as
\[ 7-0+1 \]
We now go to Step 4 and carry out the addition and subtraction in the order in which they appear. This gives us the answer:
\[ 7-0+1 =7+1 =8 \]
Using the order of operations, we can clearly see the answer is 8.
Example 8
Use the order of operations to simplify the following:
\[ 3(4-1)^2-10\div 2+3 \]
Solution
In Step 1 we simplify the expression in the parentheses:
\[ 3(3)^2-10\div 2+3 \]
Then Step 2 tells us to apply any exponents:
\[ 3\times 9 - 10\div 2+3 \]
We then go to Step 3 and apply multiplication and division in order from left to right:
\[ 27 - 5 + 3 \]
Finally, at Step 4 we carry out the addition and subtraction in order from left to right:
\[ 25 \]Examples with Variables
Example 9
When we use the order of operations in algebra, we often see variables in the expressions we need to simplify. Simplify the following expression:
\[ 3x-4(x-3)+2x \]
Solution
Step 1, we start by simplifying the expression in parentheses. In this case, \(x-3\) is already in the simplest form, so we can’t simplify it further. Step 2 doesn’t apply because there are no exponents. Step 3, perform multiplication (there is no division). We can multiply the 4 by the \(x-3\) using the distributive property to get:
\[ 3x-4x+12+2x \]
Step 4, addition and subtraction, but we can only combine like terms. This gives us \(x+12\) as the answer.Example 10
Often, instead of using the \(\div\) symbol, we write expressions as fractions. If possible, simplify the following expression:
\[ \frac{3x-4}{3} \]
Solution
It is important to realize that when an expression is written as a fraction, there are implied parentheses on the numerator and denominator of the fraction. So this expression is actually:
\[ \frac{(3x-4)}{(3)} \]
or
\[ (3x-4)\div (3) \]
This means that we have to subtract \(4\) from the \(3x\) before we can divide by \(3\) (because Step 1 tells us to perform the operation in parentheses first, including implied parentheses.) Because \(3x-4\) cannot be simplified, the entire expression is as simple as possible. Note that the \(3\) in the numerator and the \(3\) in the denominator can’t “cancel” because the order of operations with the implied parentheses in the fraction bar, tells us we must subtract 4 before we divide.Exponent Rules
Here are four important rules that tell us how to work with exponents:
| Rule 1: | \[x^ax^b=x^{a+b}\] |
| Rule 2: | \[(x^a)^b=x^{ab}\] |
| Rule 3: | \[(xy)^a=x^ay^a\] |
| Rule 4: | \[x^{-a}=\frac{1}{x^a}\] |
Note: We can apply the exponent rules in any order to simplify our answer.
Examples of Exponent Rules
Here are some examples that apply these rules.
Example 11
Simplify the following expression:
\[ \frac{(3xy)^3}{x^2} \]
Solution
First, we use Rule 2 to simplify the numerator of the fraction:
\[ \frac{3^3x^3y^3}{x^2}. \]
We know \(3^3=27\) so we can simplify:
\[ \frac{27x^3y^3}{x^2}. \]
Next, we use Rule 4 to rewrite the expression without a fraction:
\[ 27x^3y^3x^{-2}. \]
Finally, we use Rule 1 to combine the \(x\) terms:
\[ 27x^{3+(-2)}y^3. \]
This gives us the final answer:
\[ 27xy^3. \]Example 12
Simplify the following expression:
\[ \frac{2x^4(yz)^3}{(xz)^3 y^4} \]
Solution
By applying the exponent rules we get:
\[ \begin{aligned} \frac{2x^4(yz)^3}{(xz)^3 y^4} &= \frac{2x^4y^3z^3}{x^3z^3y^4}\\ &= 2x^4y^3z^3x^{-3}z^{-3}y^{-4}\\ &= 2x^{4+(-3)}y^{3+(-4)}z^{3+(-3)}\\ &= 2x^1 y^{-1} z^0\\ &=\frac{2x}{y}.\\ \end{aligned} \]Lesson Checklist
By the end of this lesson, you should be able to:
- Summarize behaviors that lead to student success.
- Perform mathematical operations with fractions (addition, subtraction, multiplication, and division).
- Apply the order of operations.
- Use the rules of exponents.
Henry B. Eyring, “Education for Real Life,” Ensign, Oct. 2002, 18-19↩︎